Haoyuan Chen

Research Fellow

National University of Singapore

Biography

I am currently a research fellow in Department of Statistics and Data Science at National University of Singapore, working with Alexandre Thiéry and Jeremy Heng. My research interests include Gaussian processes, uncertainty quantification, Bayesian learning, and probabilistic machine learning. Previously, I received my PhD in Industrial Engineering supervised by Rui Tuo and MSc in Mathematics at Texas A&M University, and BSc in Mathematics at Sichuan University.

Research Overview

My research aims to develop scalable and robust uncertainty quantification (UQ) methods for probabilistic machine learning, with a particular focus on Gaussian processes (GPs) and Bayesian learning. I develop probabilistic models that bridge the gap between rigorous statistical inference and practical applications in large-scale data and high-dimensional problems.

Research Overview for Probabilistic Machine Learning.

Research Topics

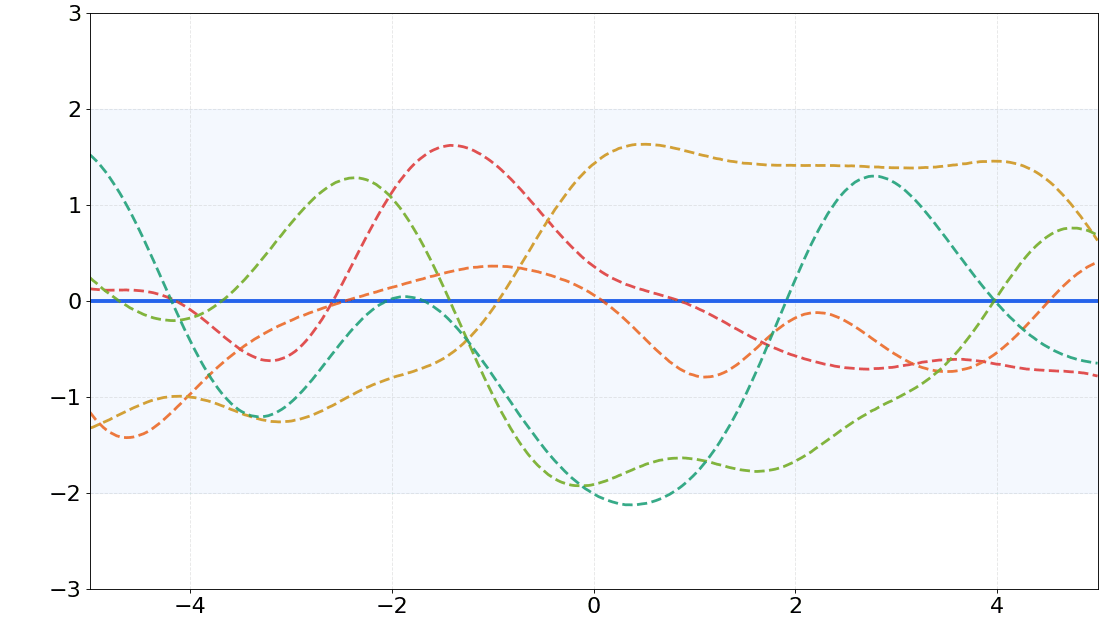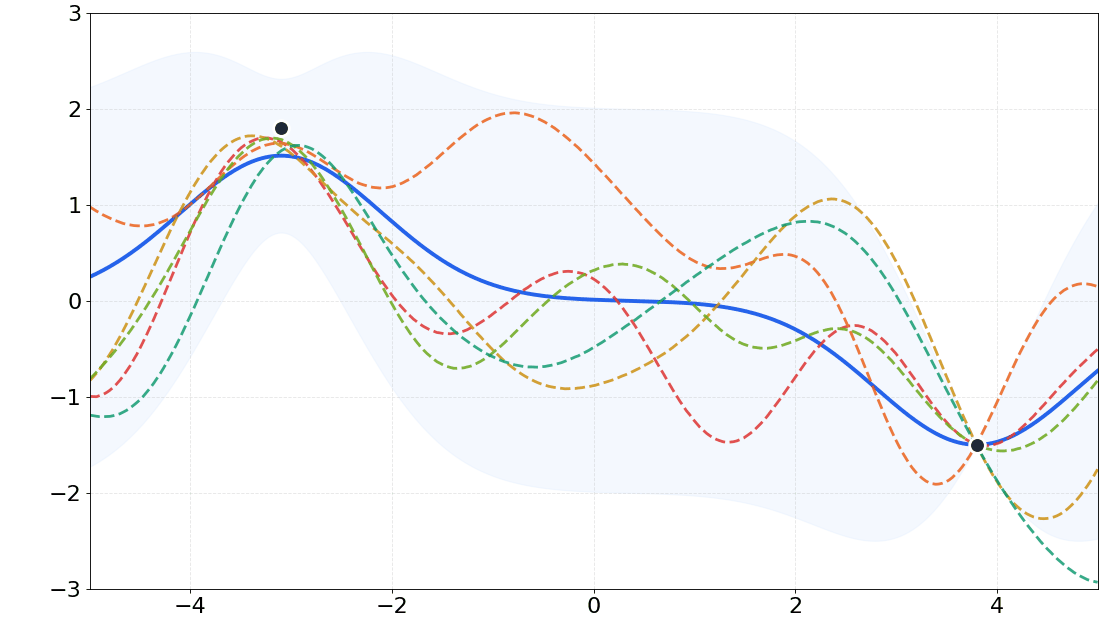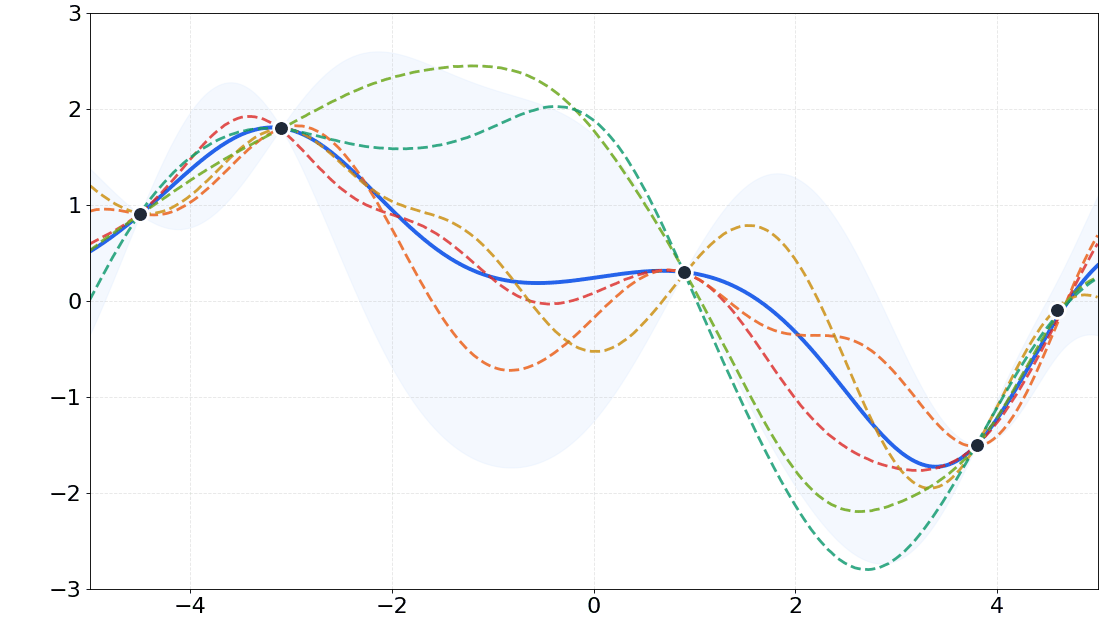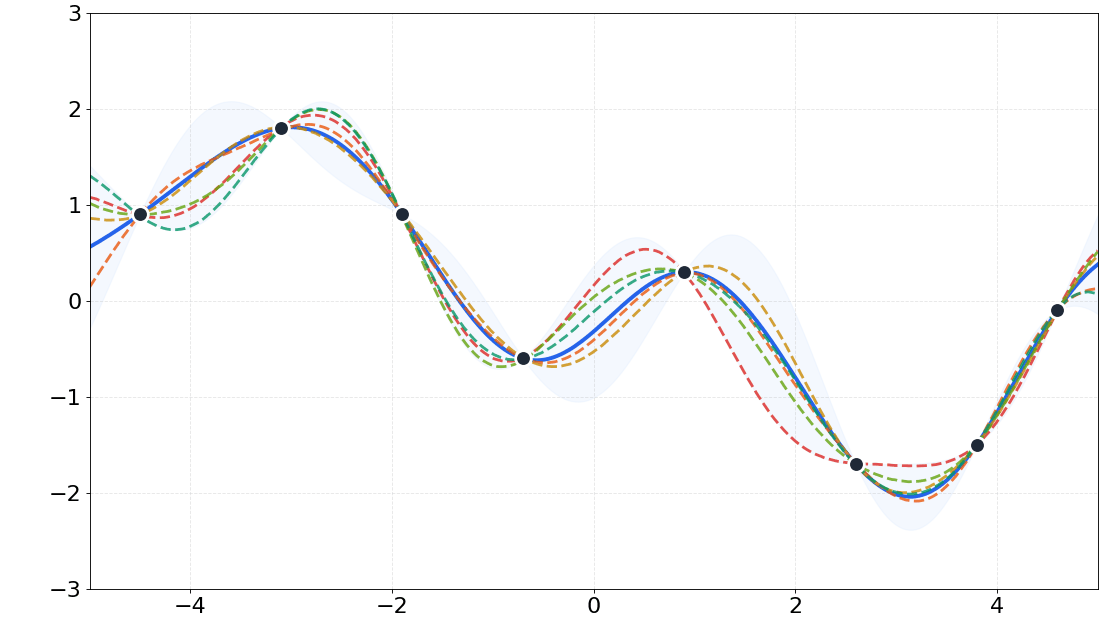
Scalable Gaussian Processes

Gaussian processes (GPs) confront significant computational bottlenecks, including the computation of the inversion and log-determinant of the covariance matrix, which limit their scalability to large datasets. These operations scale cubically with the number of data points, making standard GP inference computationally prohibitive for large datasets. Therefore, developing scalable methods for GPs is crucial to unlock their full potential for large-scale applications while preserving their desirable properties of uncertainty quantification and theoretical guarantees.

Bayesian Deep Learning

Bayesian deep learning (BDL) is a computational framework that combines Bayesian inference principles with deep learning models, offering potential to advance the current AI landscape by providing principled uncertainty quantification and improved robustness. However, BDL faces significant challenges including computational intractability due to the high-dimensional parameter spaces in neural networks, and the tendency toward overconfidence or miscalibration in posterior approximations. Therefore, addressing these computational and reliability issues is essential to make BDL practical and trustworthy in safety-critical applications.

Data Assimilation

Data assimilation (DA) combines dynamical models with sparse, noisy observations to estimate latent system states and quantify uncertainty for applications such as climate forecasting and environmental monitoring. In practice, traditional DA methods face severe challenges due to high-dimensional state spaces, nonlinear and possibly chaotic dynamics, model error arising from imperfect physical representations, and non-Gaussian uncertainties. Therefore, it is crucial to develop efficient and robust DA algorithms that can handle high-dimensional systems while properly accounting for model uncertainties for complex dynamical systems.

Real-World Applications

When applying probabilistic models to real-world problems, data complexities such as non-stationarity and heteroscedasticity can significantly degrade model performance and lead to unreliable uncertainty estimates. Non-stationarity arises when statistical properties vary across the input space, while heteroscedasticity reflects non-uniform noise levels in different regions. Therefore, it is essential to design probabilistic models and inference algorithms that explicitly handle these challenges so that the resulting systems remain robust, interpretable, and trustworthy in practical applications.